【解説】「効果を示すアウトカム指標」とは？

.

【復習】「イベント発生をアウトカムとした研究」とは？

復習として、イベント発生をアウトカムとした研究とはどのようなものなのか、Clinical Question（CQ）の型に沿って説明致します。

.

CQとは、医療従事者が日常の臨床現場で感じる漠然とした疑問のことを指します。

明確な問いの形に整えられていない段階の「臨床研究の種」とも言えるものです。

以前も述べましたが、CQは大まかに以下の４つに分けられると言われています。

.

① 病気や診療の実態を調べる研究

② 診断方法を確立する研究

③ 要因と結果との関係を調べる研究

④ 治療法 or 予防法 の効果を調べる研究

.

これらのCQのうち②を除く、①・③・④が「イベント発生をアウトカムとした研究」となりえます。

.

.

効果とは？

効果は２つ以上のものを「比較して」「その臨床的な意味付けをする」ことで初めて評価ができます。

比較の方法には以下の２種類があります。

● 「比」で見る方法

● 「差」で見る方法

.

注意が必要なのは、過去に解説した「存在を示すアウトカム指標」や「発生を示すアウトカム指標」など単独では、治療法や予防法などの効果を評価することはできないということです。

量的な臨床研究の本質は比較することです。

２つ以上のグループにおいて算出した「存在を示すアウトカム指標」や「発生を示すアウトカム指標」を比較することこそが「効果を示す」ことになります。

.

「比」で見る効果の指標

「比」で見る効果の指標としては以下のものが挙げられます。

● リスク比

● 発生率比（罹患率比）

.

.

.

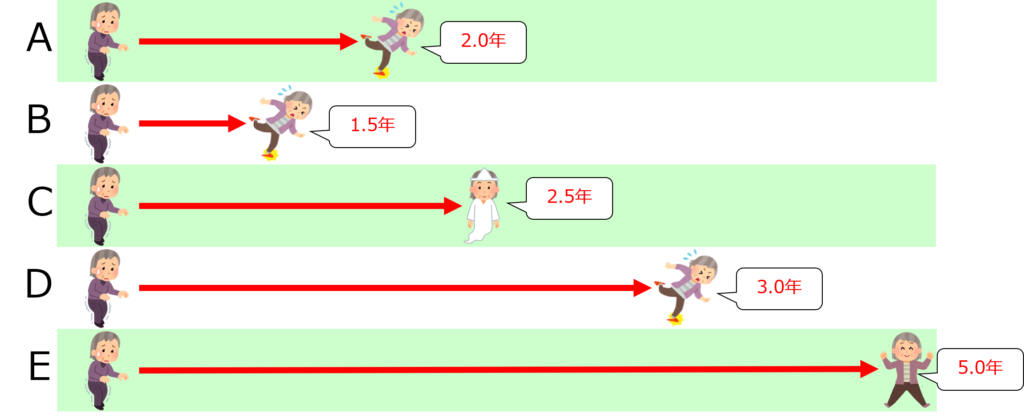
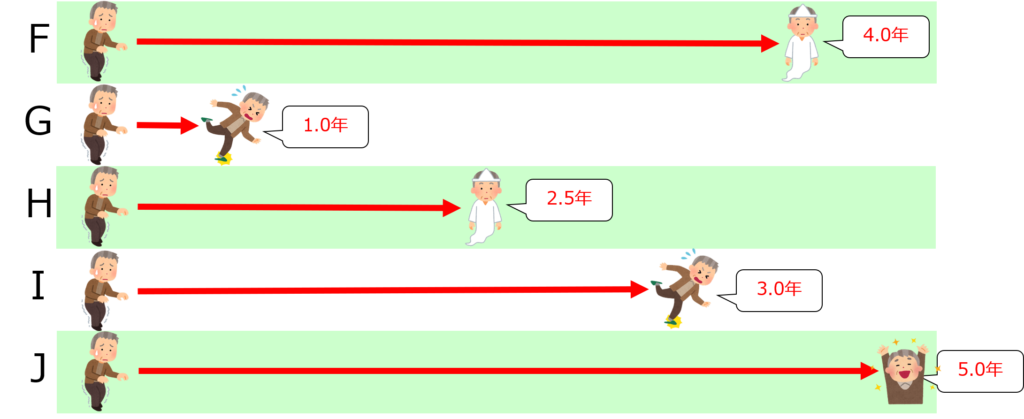
上図の「おばあさんグループ（5名）」と「おじいさんグループ（5名）」とを比較してみましょう。

それぞれ異なる転倒予防法を実施したとして、観察期間は5年間、転倒をイベント発生とします。

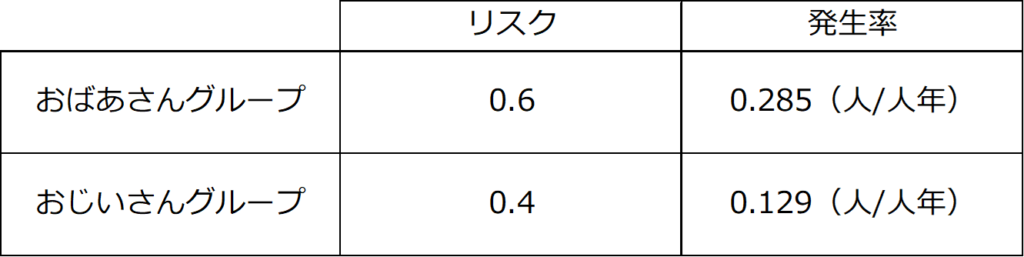
すると、それぞれのリスクと発生率は以下の通りです。

.

この場合、リスク比と発生率比は以下のようになります。

● リスク比：0.4 ÷ 0.6 = 0.66…　→　おじいさんグループが実施した転倒予防法はおばあさんグループが実施したものと比べて転倒のリスクを66%に抑えた

● 発生率比：0.129 ÷ 0.285 = 0.45…　→　おじいさんグループが実施した転倒予防法はおばあさんグループが実施したものと比べて転倒の発生率（人/人年）を45%に抑えた

.

「差」で見る効果の指標

「差」で見る効果の指標としては以下のものが挙げられます。

● リスク差

● 発生率差（罹患率差）

.

この場合、リスク比と発生率比は以下のようになります。

● リスク差：0.6 – 0.4 = 0.2　→　おじいさんグループが実施した転倒予防法はおばあさんグループが実施したものと比べて転倒のリスクを0.2だけ小さくした

● 発生率差：0.285 – 0.129 = 0.156　→　おじいさんグループが実施した転倒予防法はおばあさんグループが実施したものと比べて転倒の発生率（人/人年）を0.156（人/人年）だけ小さくした

.

「比」で見ることと「差」で見ることの違いとは？

効果を「比」で見ることと、「差」で見ることの違いは何でしょうか？

研究で得られた結果の臨床的な意義を検討するには「比」だけでなく、「差」も見ることが重要です。

例えば以下のようなケースを考えてみましょう。

● at risk な集団において1%の人に転倒が発生した

● ある転倒予防体操を実施すると転倒の発生は0.6％に減少した

.

この場合のリスク比は、0.006 ÷ 0.01 = 0.6 となります。

つまり「比」で見た場合には、転倒予防体操によって転倒の発生が60%に抑えられたということで、素晴らしく効果的な転倒予防体操だという印象を受けます。

しかし、リスク差を求めると、0.01 – 0.006 = 0.004 となります。

これは集団が1000名いたとすると、転倒した人が10名いたところが6名に減った。すなわち1000名中4名少なくなったということになります。

これだと大分、効果に対する印象が変わるのではないでしょうか？

.

このように、「比」だけで見ると効果を過大評価・過小評価してしまうことがあります。

「差」も見ることで、より冷静に効果を評価しやすくなります。

.

最後に

.

ありがとうございました!!