
備忘録として臨床研究について学んだことを記します

今回は臨床研究における誤差の分類について解説致します
.
誤差とは臨床研究の比較の質を落とすもの!!
以前投稿した「効果を示すアウトカム指標」についての記事でも触れたように、量的な臨床研究の本質は比較することです。
● ある治療法は症状の改善に有効なのか?
● ある因子がアウトカムの発生に関連しているのか?
これらも2つ以上のものを比較して差を見出すことで、有効・無効や関連の有無を判定できるのです。
.
臨床研究では、得られた結果と真実との間に必ず不一致が生じます。
これを誤差と言います。
得られた結果と真実との間の誤差の程度が大きくなるほど、研究を通じて知ろうとしていた結論が誤った形に歪められてしまいます。
.

つまり誤差とは臨床研究の比較の質を落とすものと言えるわけですね♪
結論を誤った方向へ導きかねない誤差は、臨床研究における最大の敵とも言えます。
この誤差を小さくするための工夫として、研究デザインを使う方法や、解析を使う方法が考案されてきたのです。
誤差を小さくするための方法についてはいずれ解説したいと思います。
.
誤差の分類
臨床研究において誤差とは、得られた結果と真実の値との不一致のことを指すことは先に述べました。
それでは誤差にはどのようなものがあるのでしょうか?
誤差の大まかな分類は下図のように示すことが出来ます。
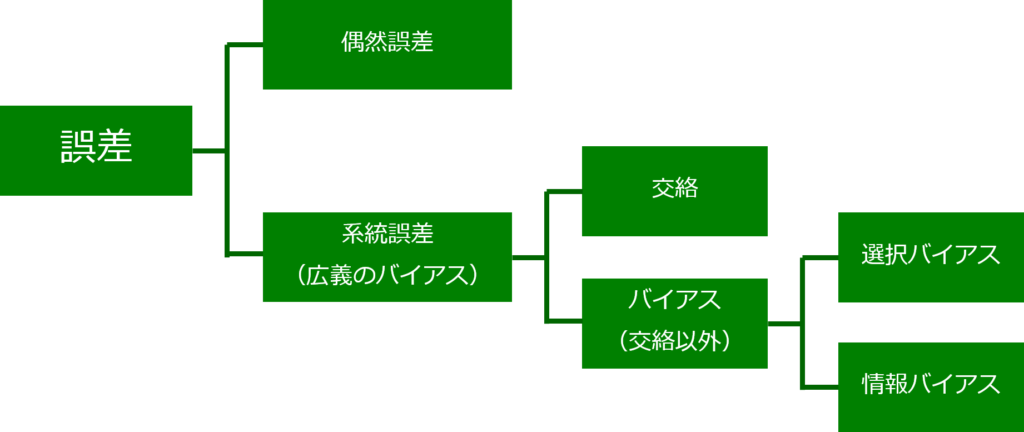
.
偶然誤差(random error)
得られる結果が真実の値に対して、高い値にも、低い値にも、どちらにも偏らずにランダムに値を取りうる場合、このような誤差は偶然誤差(random error)と言います。
例えば
● 100m走のタイムを手動のストップウォッチで計測した際の誤差(実際のゴールのタイミングよりも時計を止めるのが早くも遅くもなりうる)
● 様々なメディアの発表する内閣支持率の誤差(全国民から聴取する訳ではないので真実の値よりも高くなったり低くなったりする)
などは偶然誤差にあたります。
.
系統誤差(systematic error)
得られる結果が真実の値に対して、ある方向に一貫した(高い方ならば常に高い傾向に、低い方ならば常に低い傾向に)値を取る場合、このような誤差は系統誤差(systematic error)と言います。
● 100m走のタイムを計測する際にスタートの合図を聞いてから計測を開始してゴールラインの一歩手前にきたタイミングで計測を終了する(真実の100m走のタイムよりも必ず速いタイムになる)
● 内閣支持率を算出する際に意図的に野党支持者だけを選別して支持・不支持を聴取する(必ず内閣支持率は真実の値よりも低くなる)
などは系統誤差にあたります。
系統誤差は広い意味でバイアス(bias)と呼ばれます。
系統誤差(バイアス)には交絡と交絡以外のバイアスとに区別することが出来ます。
.
交絡(confounding)
例えば
● 高齢者は転倒予防教室に年1回参加すると転倒予防効果はあるのか?
という研究をするとします。
この場合は、転倒予防教室に参加したグループと転倒予防教室に参加しなかったグループとを追跡して、転倒の発生割合や発生率の比較をすることで検証することになります。
しかし、転倒予防教室への参加の有無以外にも様々な因子によって転倒の発生のしやすさは変わります。
年齢、運動習慣の有無、慢性疾患の有無、認知症の有無、観察開始時点の体力レベルなどが、2つのグループに明確な差がある場合は、転倒(アウトカム)の発生のしやすさに元々差があるかもしれません。
つまり、研究の中の比較で得られた差には、元々の集団が持っているアウトカムの起こしやすさの差と予防法・治療法の効果が混ざっているのです。
このような現象を交絡と言います。
.
バイアス(交絡以外)
選択バイアス(selection bias)
研究の対象者を選ぶ段階で発生する誤差を選択バイアスと言います。
選択バイアスによって、研究者が本来調査したいと考えている集団とは異なる集団の結果となってしまいます。
.
情報バイアス(information bias)
アウトカムを測定する段階で発生する誤差を情報バイアスと言います。
.
最後に

今後も臨床研究に関して学んだことを記していきたいと思います
.
ありがとうございました!!


コメント